Euclid: The reduced shear approximation and magnification bias for Stage IV cosmic shear experiments
| Authors: | A.C. Deshpande, ..., S. Casas, M. Kilbinger, V. Pettorino, S. Pires, J.-L. Starck, F. Sureau, et al. |
| Journal: | Astronomy and Astrophysics |
| Year: | 2020 |
| DOI: | 10.1051/0004-6361/201937323 |
| Download: |
Abstract
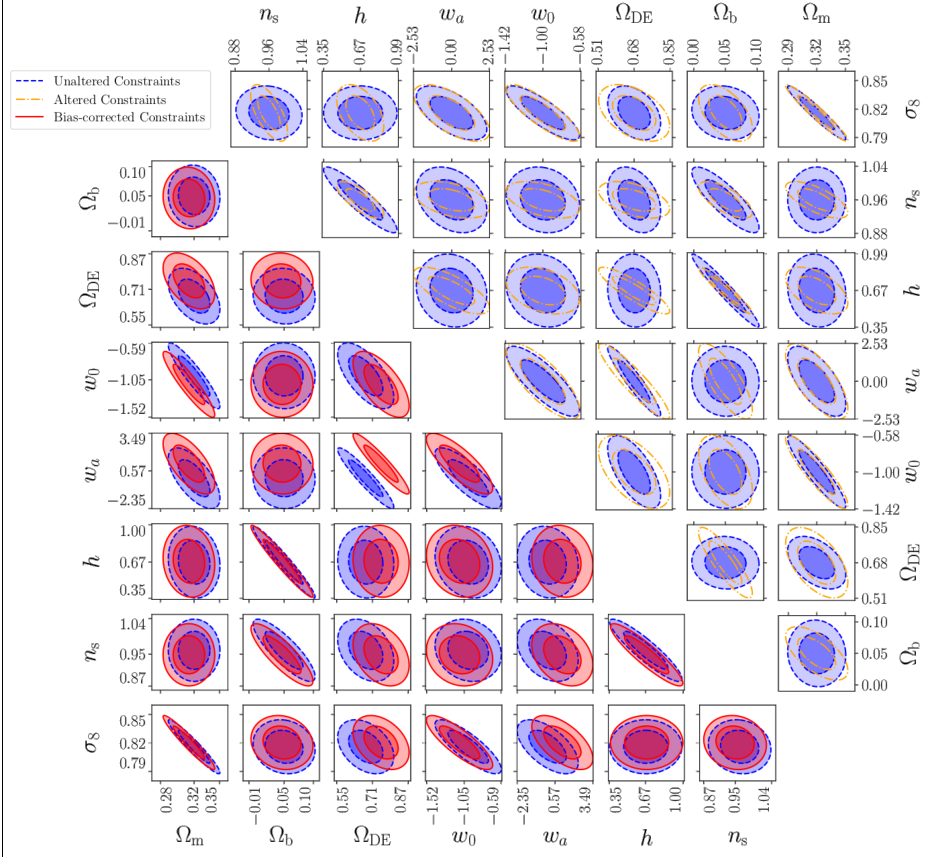
Stage IV weak lensing experiments will offer more than an order of magnitude leap in precision. We must therefore ensure that our analyses remain accurate in this new era. Accordingly, previously ignored systematic effects must be addressed. In this work, we evaluate the impact of the reduced shear approximation and magnification bias, on the information obtained from the angular power spectrum. To first-order, the statistics of reduced shear, a combination of shear and convergence, are taken to be equal to those of shear. However, this approximation can induce a bias in the cosmological parameters that can no longer be neglected. A separate bias arises from the statistics of shear being altered by the preferential selection of galaxies and the dilution of their surface densities, in high-magnification regions. The corrections for these systematic effects take similar forms, allowing them to be treated together. We calculated the impact of neglecting these effects on the cosmological parameters that would be determined from Euclid, using cosmic shear tomography. To do so, we employed the Fisher matrix formalism, and included the impact of the super-sample covariance. We also demonstrate how the reduced shear correction can be calculated using a lognormal field forward modelling approach. These effects cause significant biases in Omega_m, sigma_8, n_s, Omega_DE, w_0, and w_a of -0.53 sigma, 0.43 sigma, -0.34 sigma, 1.36 sigma, -0.68 sigma, and 1.21 sigma, respectively. We then show that these lensing biases interact with another systematic: the intrinsic alignment of galaxies. Accordingly, we develop the formalism for an intrinsic alignment-enhanced lensing bias correction. Applying this to Euclid, we find that the additional terms introduced by this correction are sub-dominant.