| Authors: | K. E. Themelis, A. A. Rontogiannis, K. D. Koutroumbas |
| Journal: | IEEE Transactions on Signal Processing |
| Year: | 2016 |
| Download: | ieeexplore |
Abstract
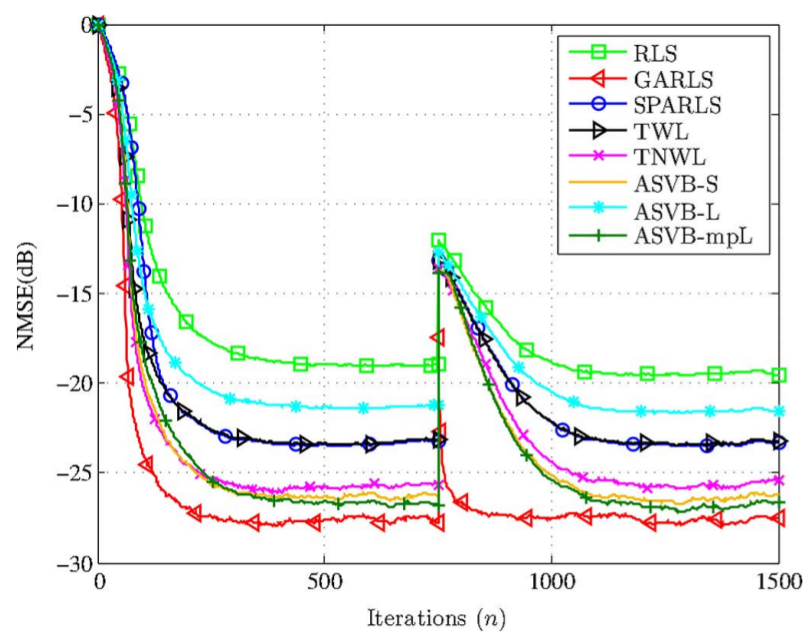
In this paper, we study the problem of time-adaptive group sparse signal estimation from a Bayesian viewpoint. We propose two online variational Bayes schemes that are specifically designed to estimate and track group sparse signals in time. The proposed schemes address both the cases where the grouping information of the signal is either known or not. For the case of known group sparsity pattern, the proposed scheme builds on a novel hierarchical model for the Bayesian adaptive group lasso. Utilizing the variational Bayes framework, update equations for all model parameters are given, for both the batch and time adaptive estimation scenarios. To address the case where the group sparsity pattern is unknown, the hierarchical Bayesian model of the former scheme is extended by organizing the penalty parameters of the Bayesian lasso in a conditional autoregressive model. Intrinsic conditional autoregression is exploited to penalize the signal coefficients in a structured manner and thus obtain group sparse solutions automatically. Again, a robust and computationally efficient online variational Bayes estimator is developed, capitalizing on the conjugacy of the proposed hierarchical Bayesian formulation. Experimental results are reported that corroborate the superior estimation performance of the proposed online schemes, when compared with state-of-the-art methods.