The primordial power spectrum describes the initial perturbations in the Universe which eventually grew into the large-scale structure we observe today, and thereby provides an indirect probe of inflation or other structure-formation mechanisms. The primordial power spectrum is therefore linked to cosmological observables and in particular the Cosmic Microwave Background (CMB). However, due to degeneracies in the transfer function that links the primordial power spectrum to the measured CMB, recovering the primordial power spectrum constitutes a non-trivial ill-posed inverse problem. Furthermore, the multiplicative nature of the noise on the estimator of CMB power spectrum adds to the complexity of the problem. PRISM is a new sparsity-based, non-linear reconstruction technique which aims at reconstructing global and local features on the primordial power spectrum from CMB measurements. Features are detected and reconstructed based on their significance compared to noise. The PRISM software is part of the ISAP package and will be included in the next release of the package.
The algorithm
The primordial power spectrum reconstruction problem is an ill-posed linear inverse problem which we address through the framework of sparse regularisation. This framework allows for accurate and robust recovery by leveraging a sparsity prior on the signal to recover (i.e. it is assumed that it can be represented using a small number of coefficients in an adapted dictionary). Formally, the observed pseudo-power spectrum $$\widetilde{C}_\ell$$ computed from masked CMB maps can be linked to the underlying primordial power spectrum $$P_k$$ through a linear relation of the form: \[\widetilde{C}_\ell = \left( \mathbf{M} P_k \right) Z_\ell \] where $$\mathbf{M}$$ is a linear operator that encodes the angular transfer function of CMB anisotropies and the effects of masks and beams, and $$\mathbf{Z_\ell}$$ is a multipicative noise term. The recovery of the primordial power spectrum is performed by solving an optimization problem of the form: \[\min\limits_{X} \quad \frac{1}{2} \underbrace{\parallel C_\ell – \mathbf{M} X \parallel^{2}_{2}}_{\mbox{data fidelity term}} \quad + \quad \lambda \underbrace{\parallel \mathbf{\Phi} X \parallel_{1}}_{\mbox{sparsity promoting term}} \] where $$\mathbf{\Phi}$$ is a wavelet transform. To estimate the unknown quantity $$C_\ell – \mathbf{M} X$$ from the noisy quantity $$\widetilde{C}_\ell – \mathbf{M} X$$, we use a variance stabilisation approach derived from the technique used in the TOUSI algorithm (Paykari et al. (2012)) and based on the Whaba variance stabilisation transform.
Results on simulations
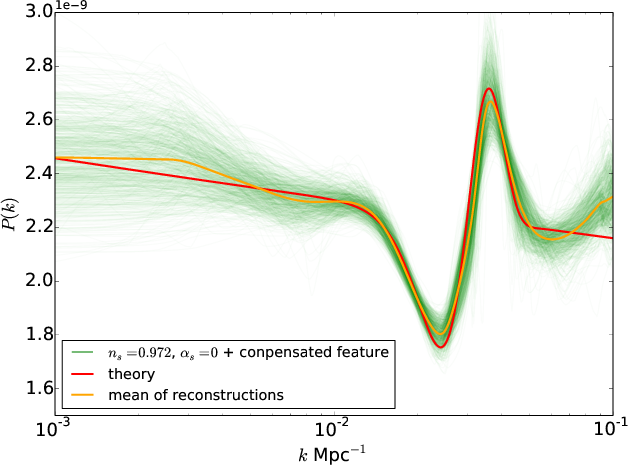
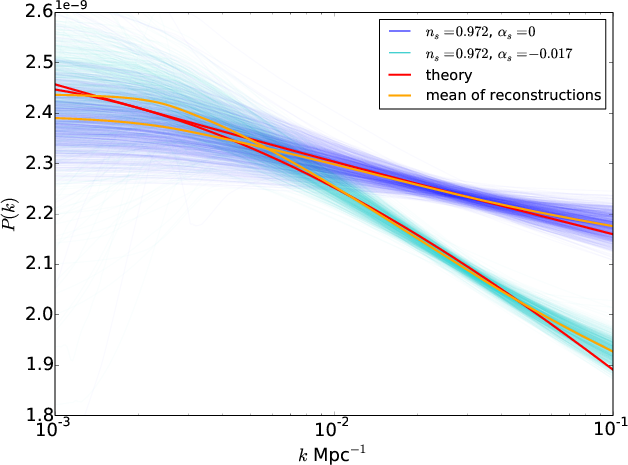
To assess the performance of PRISM we produced a large number of Monte-Carlo CMB simulations for different test power spectra. We tested a near scale invariant primordial power spectra with ns=0.972, a power spectrum with a running of the spectral index with ns=0.972, $$\alpha_s$$= -0.017 (see Figure 2), and a power law spectrum with a localised feature around 0.3 Mpc (see Figure 1).
Publications
- Lanusse, F., Paykari, P., Starck, J.-L., Sureau, S., Bobin, J., Rassat, A., PRISM: Recovery of the primordial spectrum from Planck data. Astronomy and Astrophysics , Accepted, 2014.
- Paykari, P., Lanusse, F., Starck, J.-L., Sureau, F., Bobin, J., PRISM: Sparse recovery of the primordial power spectrum , Astronomy and Astrophysics , 566, id.A77, pp 10, 2014.

