Constraining neutrino masses with weak-lensing multiscale peak counts

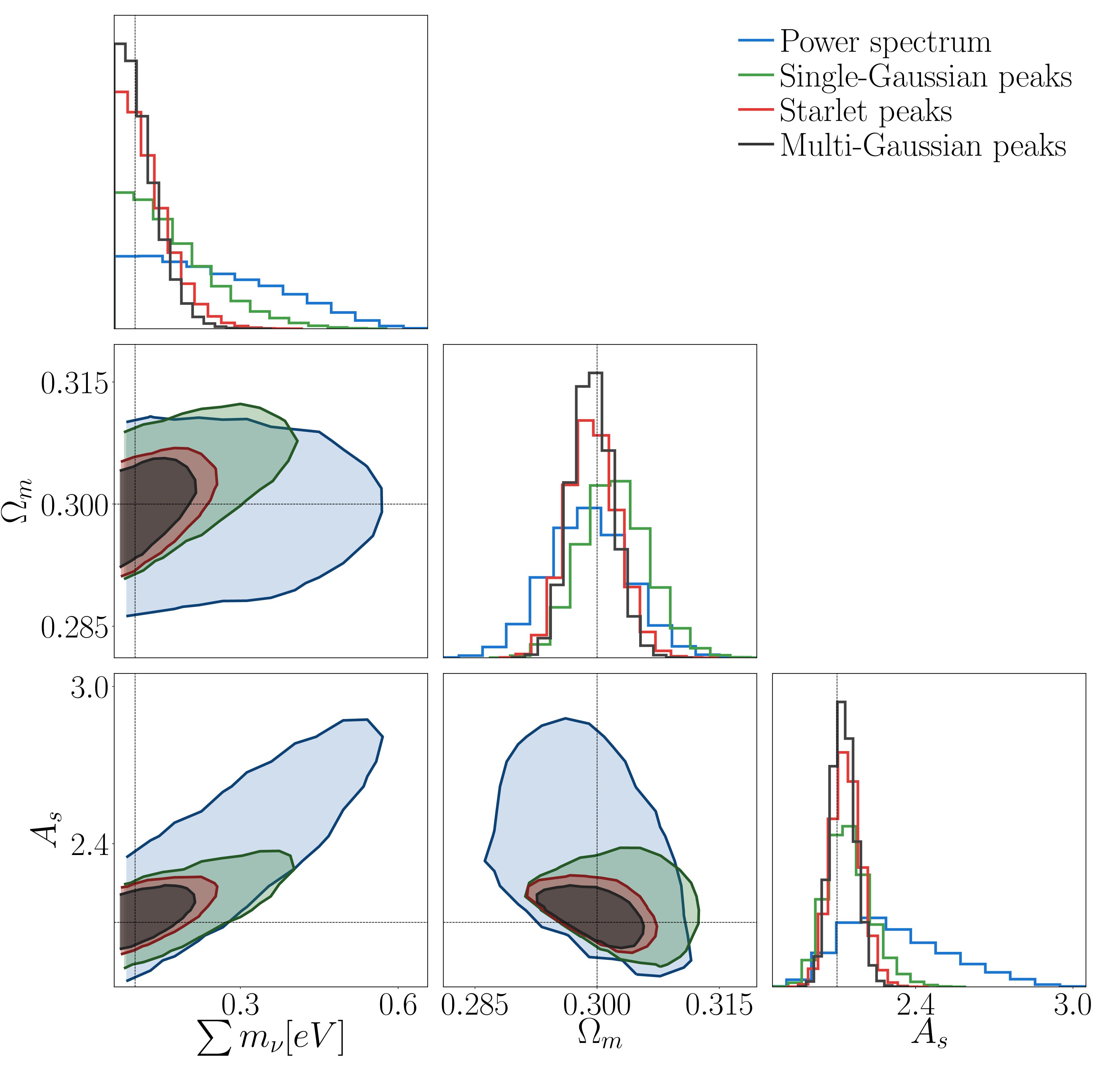
Massive neutrinos influence the background evolution of the Universe as well as the growth of structure. Being able to model this effect and constrain the sum of their masses is one of the key challenges in modern cosmology. Weak-lensing cosmological constraints will also soon reach higher levels of precision with next-generation surveys like LSST, WFIRST and Euclid. In this context, we use the MassiveNus simulations to derive constraints on the sum of neutrino masses Mν , the present- day total matter density Ωm, and the primordial power spectrum normalization As in a tomographic setting. We measure the lensing power spectrum as second-order statistics along with peak counts as higher-order statistics on lensing convergence maps generated from the simulations. We investigate the impact of multi-scale filtering approaches on cosmological parameters by employing a starlet (wavelet) filter and a concatenation of Gaussian filters. In both cases peak counts perform better than the power spectrum on the set of parameters [Mν, Ωm, As] respectively by 63%, 40% and 72% when using a starlet filter and by 70%, 40% and 77% when using a multi-scale Gaussian. More importantly, we show that when using a multi-scale approach, joining power spectrum and peaks does not add any relevant information over considering just the peaks alone. While both multi-scale filters behave similarly, we find that with the starlet filter the majority of the information in the data covariance matrix is encoded in the diagonal elements; this can be an advantage when inverting the matrix, speeding up the numerical implementation. For the starlet case, we further identify the minimum resolution required to obtain constraints comparable to those achievable with the full wavelet decomposition and we show that the information contained in the coarse-scale map cannot be neglected.