Effect of inhomogeneities on high precision measurements of cosmological distances

Abstract

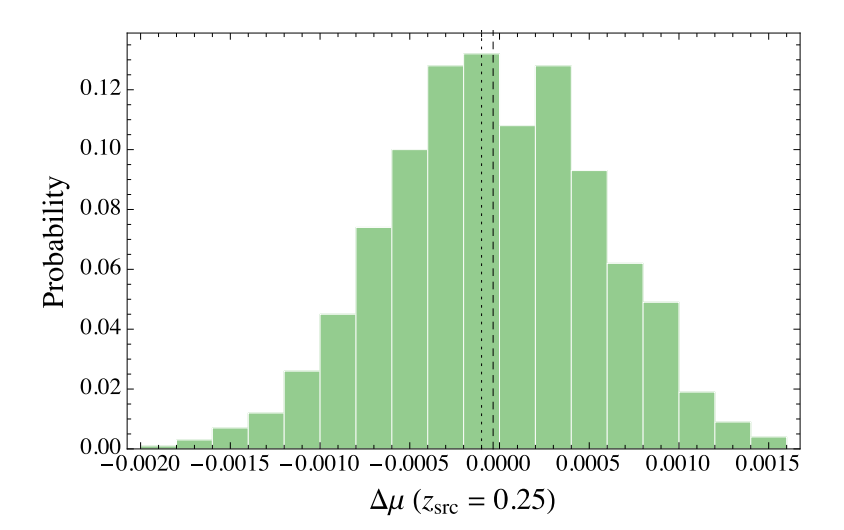
We study effects of inhomogeneities on distance measures in an exact relativistic Swiss-cheese model of the Universe, focusing on the distance modulus. The model has Λ CDM background dynamics, and the "holes" are nonsymmetric structures described by the Szekeres metric. The Szekeres exact solution of Einstein's equations, which is inhomogeneous and anisotropic, allows us to capture potentially relevant effects on light propagation due to nontrivial evolution of structures in an exact framework. Light beams traversing a single Szekeres structure in different ways can experience either magnification or demagnification, depending on the particular path. Consistent with expectations, we find a shift in the distance modulus μ to distant sources due to demagnification when the light beam travels primarily through the void regions of our model. Conversely, beams are magnified when they propagate mainly through the overdense regions of the structures, and we explore a small additional effect due to time evolution of the structures. We then study the probability distributions of Δ μ = μ_ΛCDM-μ_SC for sources at different redshifts in various Swiss-cheese constructions, where the light beams travel through a large number of randomly oriented Szekeres holes with random impact parameters. We find for Δμ the dispersions 0.004 ≤ σ_Δμ ≤ 0.008 mag for sources with redshifts 1.0 ≤ z ≤ 1.5 , which are smaller than the intrinsic dispersion of, for example, magnitudes of type Ia supernovae. The shapes of the distributions we obtain for our Swiss-cheese constructions are peculiar in the sense that they are not consistently skewed toward the demagnification side, as they are in analyses of lensing in cosmological simulations. Depending on the source redshift, the distributions for our models can be skewed to either the demagnification or the magnification side, reflecting a limitation of these constructions. This could be the result of requiring the continuity of Einstein's equations throughout the overall spacetime patchwork, which imposes the condition that compensating overdense shells must accompany the underdense void regions in the holes. The possibility to explore other uses of these constructions that could circumvent this limitation and lead to different statistics remains open.