Abstract
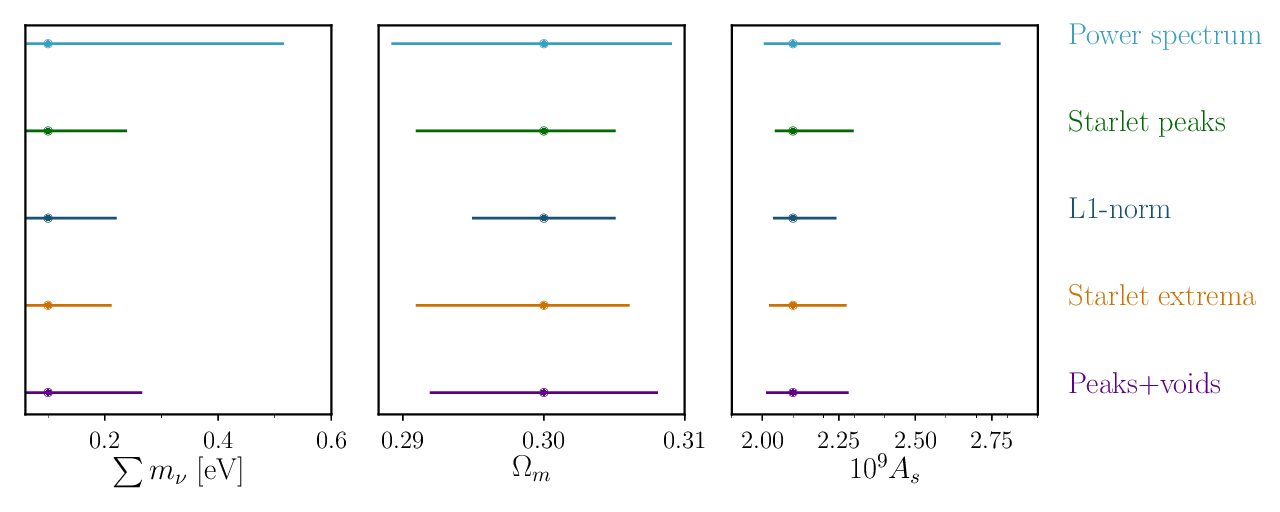
We present a new summary statistic for weak lensing observables, higher than second order, suitable for extracting non-Gaussian cosmological information and inferring cosmological parameters. We name this statistic the 'starlet ℓ1-norm' as it is computed via the sum of the absolute values of the starlet (wavelet) decomposition coefficients of a weak lensing map. In comparison to the state-of-the-art higher-order statistics -- weak lensing peak counts and minimum counts, or the combination of the two -- the ℓ1-norm provides a fast multi-scale calculation of the full void and peak distribution, avoiding the problem of defining what a peak is and what a void is: The ℓ1-norm carries the information encoded in all pixels of the map, not just the ones in local maxima and minima. We show its potential by applying it to the weak lensing convergence maps provided by the MassiveNus simulations to get constraints on the sum of neutrino masses, the matter density parameter, and the amplitude of the primordial power spectrum. We find that, in an ideal setting without further systematics, the starlet ℓ1-norm remarkably outperforms commonly used summary statistics, such as the power spectrum or the combination of peak and void counts, in terms of constraining power, representing a promising new unified framework to simultaneously account for the information encoded in peak counts and voids. We find that the starlet ℓ1-norm outperforms the power spectrum by 72% on Mν, 60% on Ωm, and 75% on As for the Euclid-like setting considered; it also improves upon the state-of-the-art combination of peaks and voids for a single smoothing scale by 24% on Mν, 50% on Ωm, and 24% on As.