| Authors: | A. Labatie, J-L. Starck, M. Lachièze-Rey, P. Arnalte-Mur |
| Journal: | arXiv |
| Year: | 2010 |
| Download: | ADS | arXiv |
Abstract
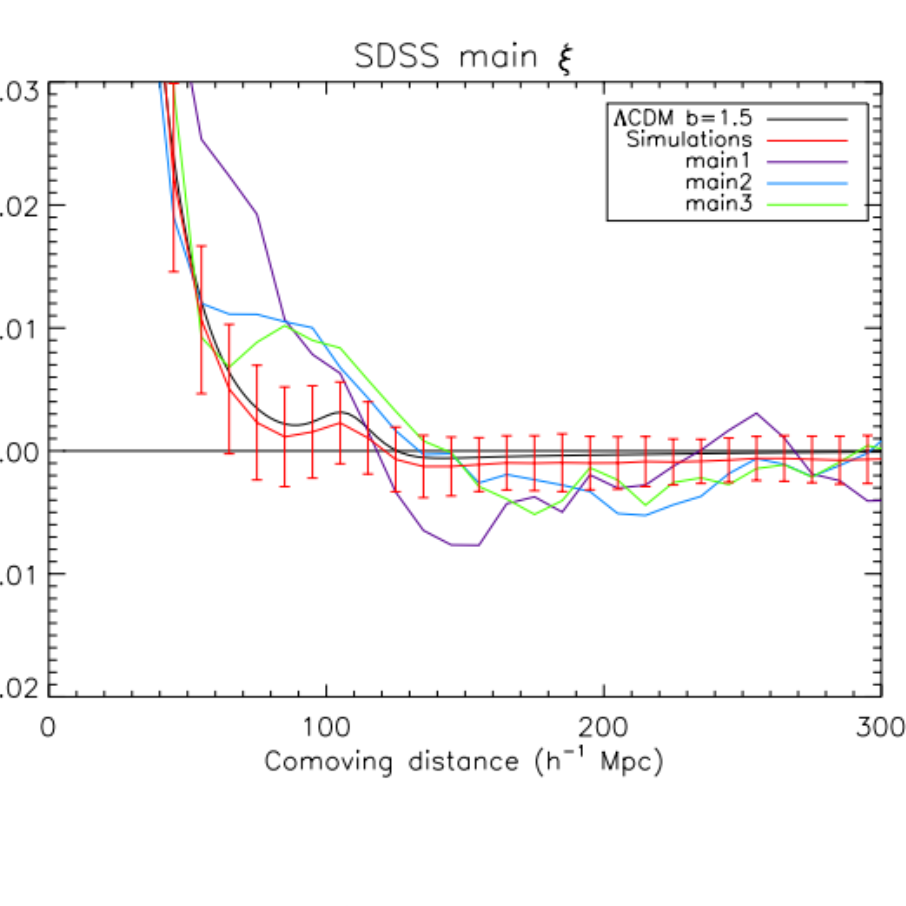
We study the uncertainty in different two-point correlation function (2PCF) estimators in currently available galaxy surveys. This is motivated by the active subject of using the baryon acoustic oscillations (BAOs) feature in the correlation function as a tool to constrain cosmological parameters, which requires a fine analysis of the statistical significance. We discuss how estimators are affected by both the uncertainty in the mean density n¯ and the integral constraint 1V2∫V2ξ̂ (r)d3r=0 which necessarily causes a bias. We quantify both effects for currently available galaxy samples using simulated mock catalogues of the Sloan Digital Sky Survey (SDSS) following a lognormal model, with a Lambda-Cold Dark Matter (ΛCDM) correlation function and similar properties as the samples (number density, mean redshift for the ΛCDMcorrelation function, survey geometry, mass-luminosity bias). Because we need extensive simulations to quantify small statistical effects, we cannot use realistic N-body simulations and some physical effects are neglected. Our simulations still enable a comparison of the different estimators by looking at their biases and variances. We also test the reliability of the BAO detection in the SDSS samples and study the compatibility of the data results with our ΛCDM simulations.
Summary
We have investigated whether Labini's group claim, that the 2PCF at large scales behavior in galaxy surveys (BAO, Universe homogenization) cannot be trusted due to the limited volume effect, is correct. We have demonstrated that all 2PCF estimators verifies a relation called integral constraint, which is not necessary by the real 2PCF, which biases correlation function estimators. But we showed using simulations of the Sloan Digital Sky Survey Data Release 7 (SDSS DR7) that the effect of the constraint is very small for current galaxy surveys (Labatie, Starck, Lachieze-Rey, Statistical Methodology, 2011).